Entendendo o algoritmo Minimax com o Jogo da Velha
Robot chatbot vector created by upklyak - www.freepik.com
Bom dia, Boa tarde ou Boa noite (dependendo da hora que você está lendo esse artigo), nesse post vamos entender um pouco melhor o algoritmo Minimax. Vamos também ver como ele funciona com um exemplo prático de aplicação ao jogo da velha.
Antes de tudo, para que você possa aproveitar melhor o centeúdo, é interessante que você tenha o interpretador de Python instalado no seu computador e entenda:
- O básico da linguagem Python:
- Variáveis e tipos de dados
- Estruturas de condição e repetição
- Funções
- Sobre recursividade e como funciona
- O básico sobre árvores e estrutura de dados
Se interessou? Pois, segue o fio e vamos em frente porque atrás vem gente.
Vá direto ao assunto...
Preparando o jogo da velha
O jogo da velha, cerquilha, jogo do galo ou tic-tac-toe é um jogo/passatempo muito popular (joguei muito quando era pequeno). Ele possui regras bem simples. A ideia geral é que tendo um tabuleiro 3 x 3, cada jogador escolhe um símbolo, tipicamente "X" ou "O", e cada um dele faz uma jogada por turno. O jogador que conseguir colocar 3 símbolos iguais em linha, coluna ou diagonal vence o jogo. Caso isso não seja possível e as jogadas se esgotem, o jogo acaba em empate.
Bom, para que possamos implementar o nosso algoritmo invencível no jogo da velha, precisamos primeiro ter um jogo da velha (hehehehe). Então, vamos contruir uma versão bem simples utilizando Python e deixá-lo pronto para que possamos enfrentar o computador.
Vamos precisar de algumas funções úteis:
- Função para verificar se um determinado jogador venceu
- Função para verificar se houve empate
- Função para verificar se o jogo acabou
- Por último, uma função para imprimir na tela o nosso tabuleiro
Após implementar-mos essas funções é só montar a lógica do nosso jogo.
Vamos começar com a função para determinar um vencedor:
def is_win(board, player):
# Verificando as Linhas do Tabuleiro
if board[0][0] == player and board[0][1] == player and board[0][2] == player:
return True
if board[1][0] == player and board[1][1] == player and board[1][2] == player:
return True
if board[2][0] == player and board[2][1] == player and board[2][2] == player:
return True
# Verificando as Colunas do Tabuleiro
if board[0][0] == player and board[1][0] == player and board[2][0] == player:
return True
if board[0][1] == player and board[1][1] == player and board[2][1] == player:
return True
if board[0][2] == player and board[1][2] == player and board[2][2] == player:
return True
# Verificando as Diagonais do Tabuleiro
if board[0][0] == player and board[1][1] == player and board[2][2] == player:
return True
if board[2][0] == player and board[1][1] == player and board[0][2] == player:
return True
return False
Eu sei que tem muitos IFs, mas eu tentei fazer da forma mais didática possível para facilitar o entendimento. Basicamente estamos verificando todas as linhas, colunas e diagornais, para checar se o player formou uma sequência. Em caso positivo retornamos True, e False caso contrário.
Em seguida precisamos verificar o empate:
def is_draw(board):
for line in board:
if ' ' in line:
return False
return True
Para definir se houve empate ou não, basta ver todas as linha, se houver algum espaço em branco significa que o jogo ainda não acabou. Em seguida vamos definir uma função para verificar se o jogo foi finalizado:
def is_terminal(board):
if is_win(board, CPU_PLAYER) or is_win(board, HUMAN_PLAYER) or is_draw(board):
return True
return False
Essa função vai nos ajudar a simplificar o nosso código e também vai ser útil quando estivermos implementando o Minimax. Ainda não se preocupe com as variáveis CPU_PLAYER e HUMAN_PLAYER, elas serão definidas em outro momento, apenas pense nelas como o símbolo que identifica cada jogador, no nosso caso X e O.
Por último, mas não menos importante, precisamos da função que vai desenhar o nosso tabuleiro:
def print_board(board):
print('\n')
for i, line in enumerate(board):
print(*line, sep=' | ')
if i != len(line) - 1:
print('--+---+--')
print('\n')
Com as funções necessárias já finalizadas, agora podemos montar a nossa lógica de jogo.
from random import randint
# ...
# AQUI FICARIAM AS OUTRAS FUNÇÔES
# ...
if __name__ == '__main__':
CPU_PLAYER = 'X'
HUMAN_PLAYER = 'O'
human_play_first = input('Você deseja começar o jogo [s|n]: ') == 's'
if human_play_first:
HUMAN_PLAYER = 'X'
CPU_PLAYER = 'O'
board = [[' ', ' ', ' '],
[' ', ' ', ' '],
[' ', ' ', ' ']]
while not is_terminal(board):
if human_play_first:
print_board(board)
position = int(input('Insira a posição da jogada [1-9]: '))
i = (position - 1) // 3
j = (position - 1) % 3
board[i][j] = HUMAN_PLAYER
if is_terminal(board):
break
i, j = randint(0, 2), randint(0, 2)
while board[i][j] != ' ':
i, j = randint(0, 2), randint(0, 2)
board[i][j] = CPU_PLAYER
human_play_first = True
print_board(board)
Com a lógica de jogo finalizada, sinta-se a vontade para testar. Nessa parte, enquanto não temos o nosso algoritmo inteligente, fazemos o computador realizar jogadas aleatórias com o trecho:
i, j = randint(0, 2), randint(0, 2)
while board[i][j] != ' ':
i, j = randint(0, 2), randint(0, 2)
board[i][j] = CPU_PLAYER
Se for da sua preferência você ainda pode colocar um trecho, após a última função print_board, para entregar uma mensagem amigável ao usuário, como ilustrado abaixo.
if is_win(board, HUMAN_PLAYER):
print('Você venceu!!')
elif is_win(board, CPU_PLAYER):
print('Você perdeu!!')
else:
print('Deu Empate!!')
O código completo dessa parte do jogo da velha você pode encontrar nesse link.
Bom, código implementado e tudo funcional, está na hora de pensar em deixar o nosso computador um pouco mais inteligente.
O Minimax
O Minimax é um algoritmo baseado em árvore que trabalha de forma recursiva e é utilizado em teoria da decisão e teoria dos jogos. Ele fornece um movimento ótimo para o jogador, considerando que o oponente também joga de forma ótima. Ele geralmente é utilizado para implementar IA em jogos, como Xadrez, Jogo da Velha, e vários outros jogos de dois jogadores.
O Minimax intuitivamente constrói uma árvore para a tomada de decisão levando em consideração todas as jogadas possíveis. Essa árvore muitas vezes é difícil de ser percebida, dado que ela é feita através de recursividade, onde muita abstração é necessária.
Todos os nossos exemplos de utilização do Minimax vão levar em consideração o jogo da velha.
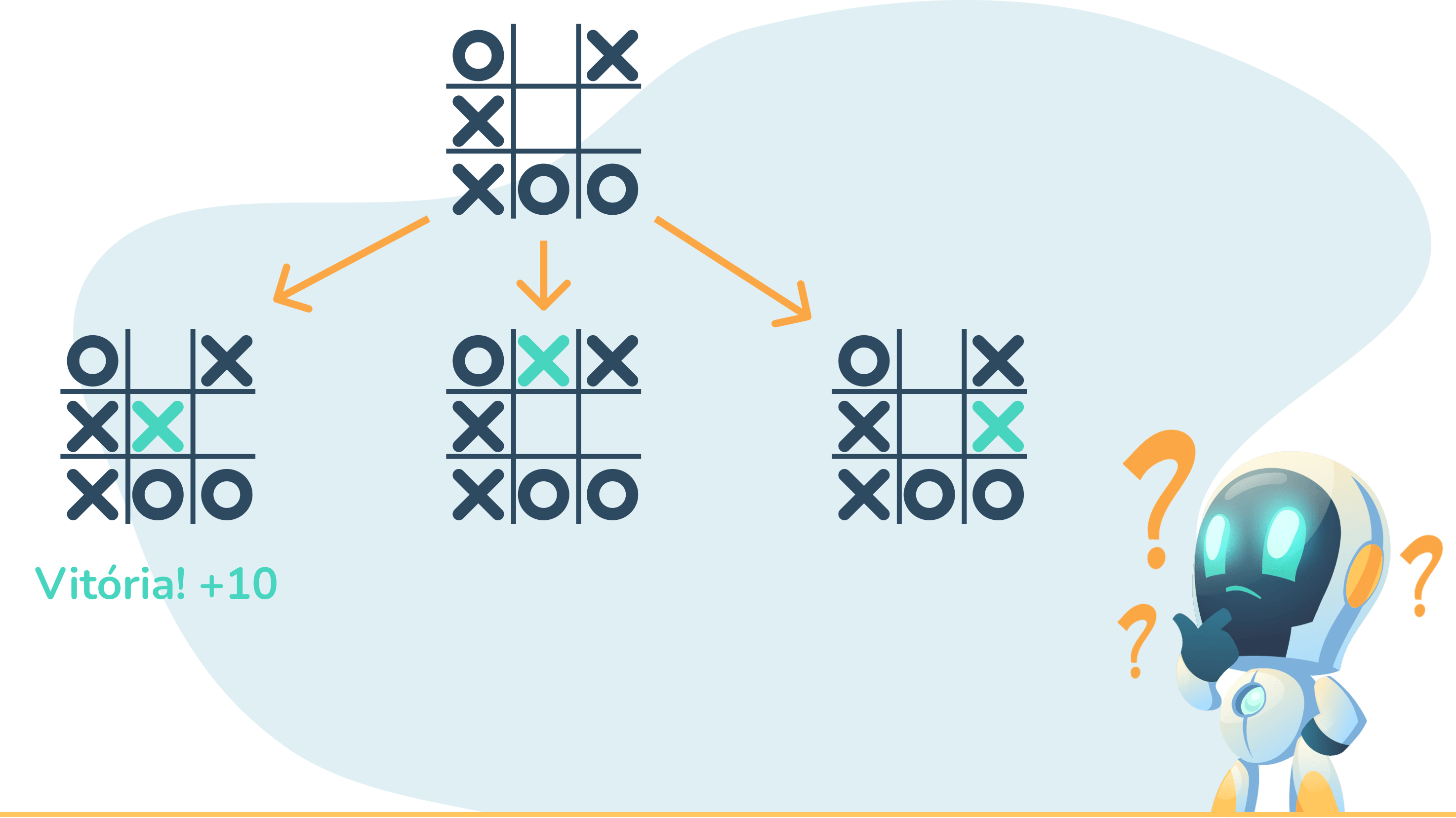
Imagine a seguinte situação, o seu nome é MAX e o seu oponente se chama MIN. Você está em um jogo bem complicado e é a sua vez. Uma forma comum de pensar seria: Se eu, MAX jogar na posição x, o MIN pode jogar em y ou z, e dai então eu...
Esse tipo de pensamento pode ser modelado como uma árvore de decisão como visto abaixo.
Olhando dessa forma, podemos escolher uma jogada e saber exatamente quais as consequências dessa escolha.
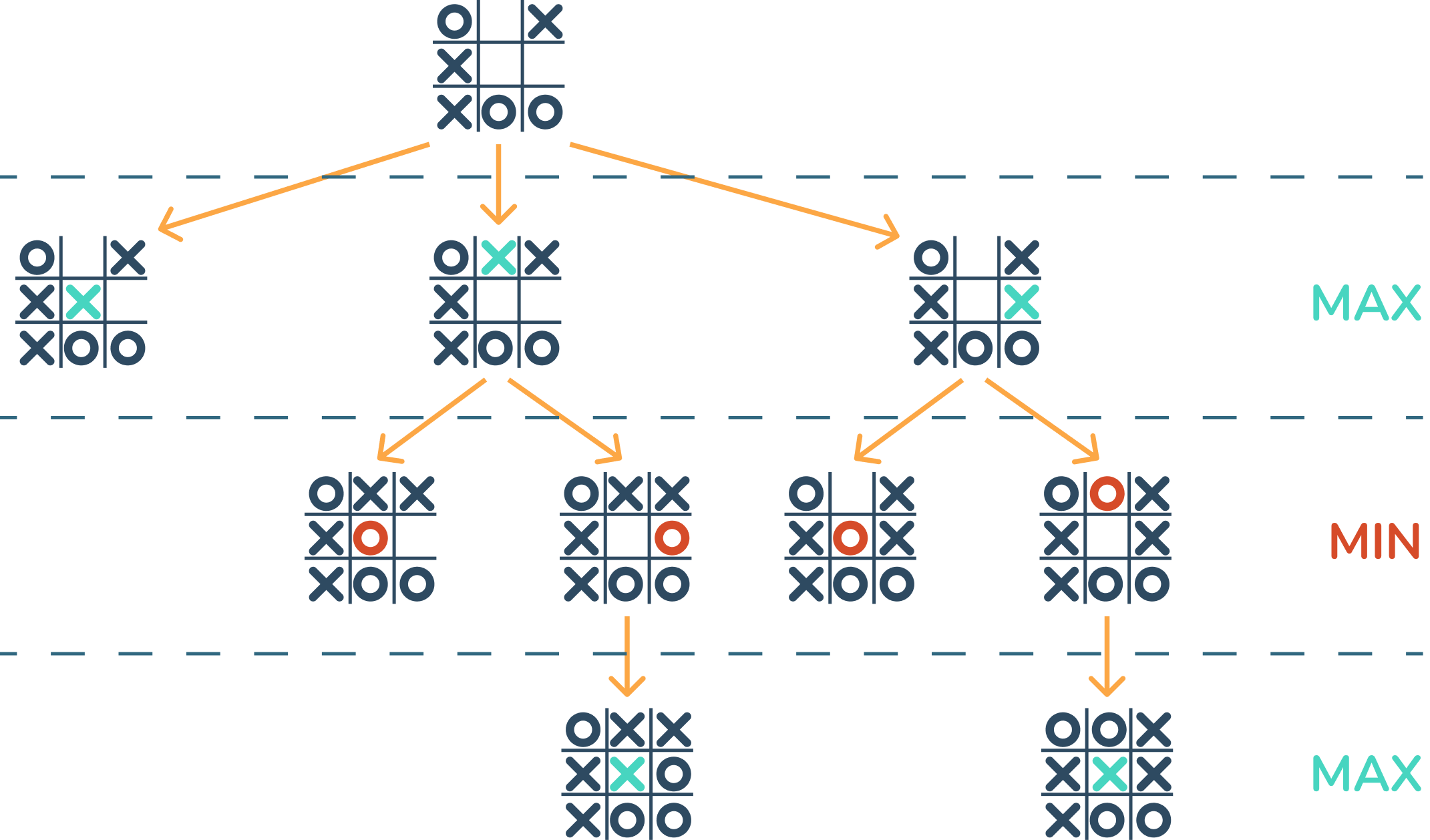
Agora precisamos de alguma forma identificar onde o jogo termina e atribuir uma pontuação adequada. No nosso caso vamos colocar +1 sempre que o MAX vencer, -1 para o caso de vitória do MIN e 0 no empate. Essas pontuações podem ser alteradas, mas é importante de alguma forma fazer com que a vitória seja mais vantajosa que a derrota. Assim, para representar essa importância colocamos números positivos, negativos e neutros, introduzindo então, uma lógica matemática.
No caso do nosso exemplo não tivemos situações de empate, mas é importante sempre lembrar de colocar todas as pontuações corretas.
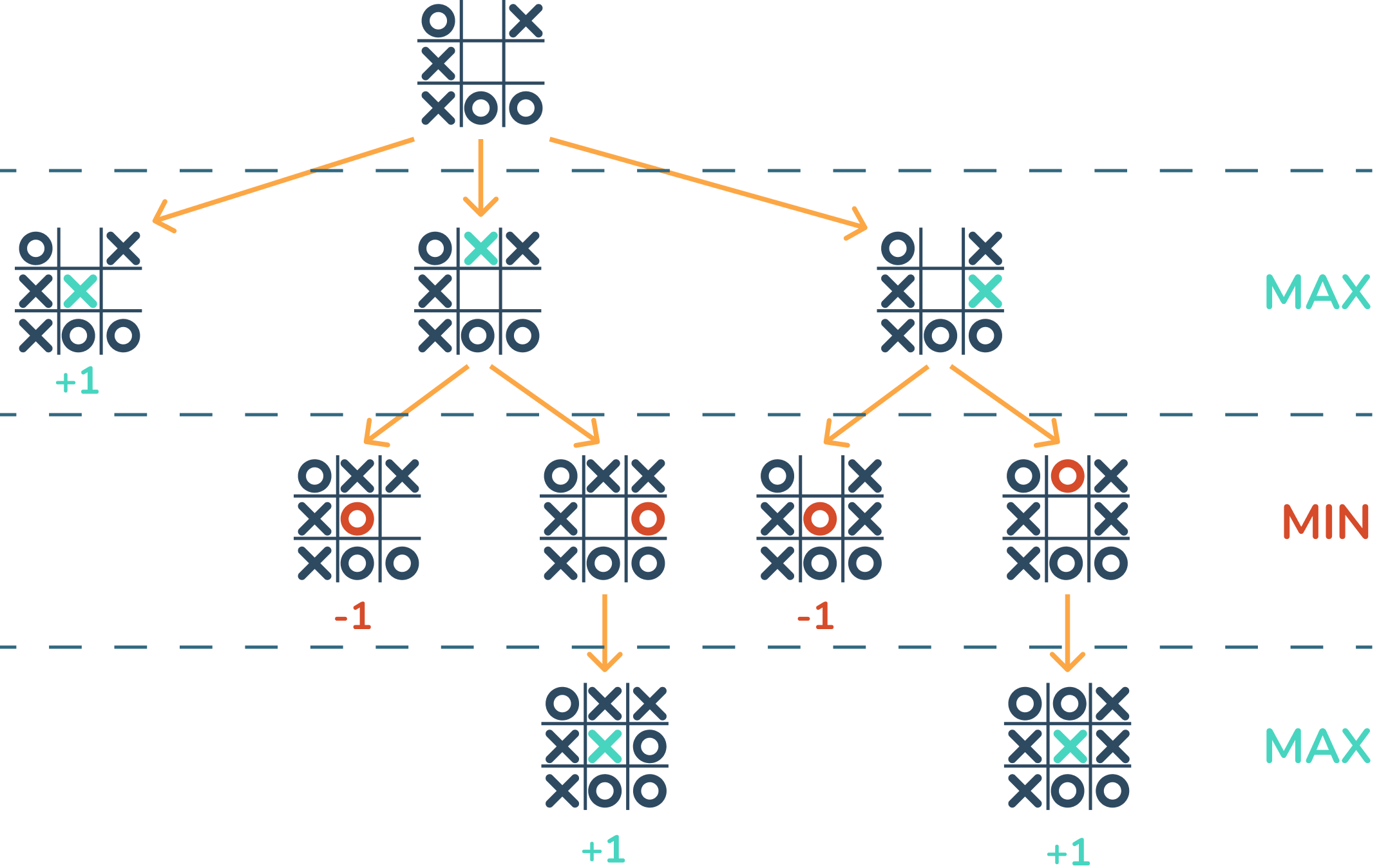
Agora vamos propagar a nossa pontuação para os estados superiores para saber qual é a melhor jogada para escolher. Pense agora que sempre que o MAX vai fazer a jogada ele quer maximizar as suas chances e por isso sempre escolhemos a maior pontuação para ser propagada. Já no caso da jogada do MIN, ele quer minimizar as chances do MAX e assim sempre escolhe a menor pontuação a ser propagada.
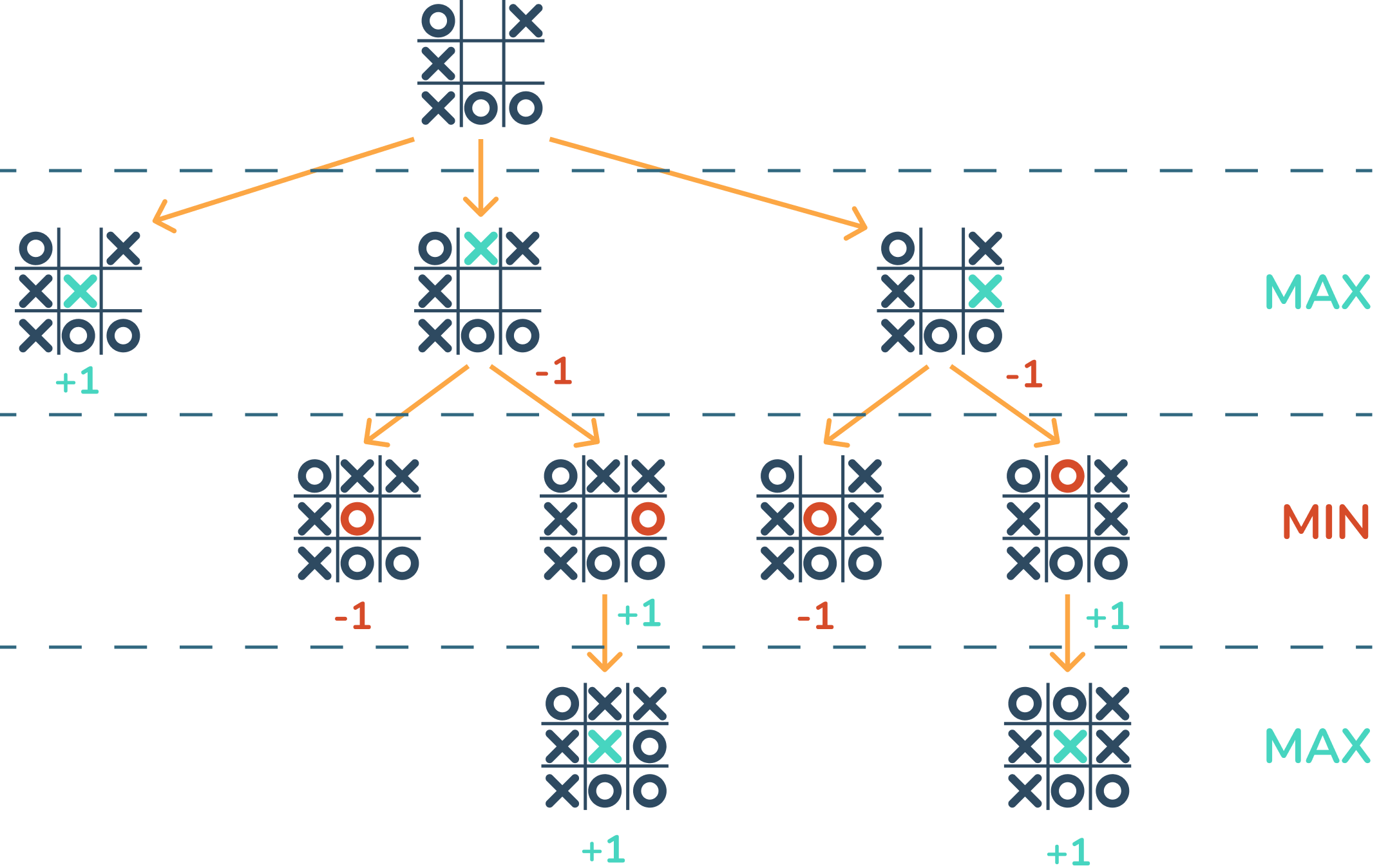
Agora o MAX tem 3 possibilidades de escolha, uma com pontuação +1 e duas com -1. Como o MAX é esperto e quer sempre escolher a melhor jogada possível, a jogada escolhida será a demonstrada abaixo. Assim, como consequência dessa escolha, o MAX vence o jogo.

Seguindo esse exemplo nós acabamos de definir o comportamento esperado do Minimax.
Sendo uma pessoa esperta, imagino que você deve ter notado que se em algum estado a pontuação estiver negativa, significa que em algum momento na subárvore existe pelo menos uma possibilidade de derrota. Deve ter percebido também que só é interessante seguir esse caminho quando não temos nenhuma opção melhor como uma vitória ou um empate. De forma análoga, se existe um ramo com pontuação positiva, significa que naquela subárvore existe 100% de chance de vitória.
Com a lógica de funcionamento já definida, podemos enfim tentar implementar esse algoritmo no nosso jogo.
Implementando a abordagem ingênua
Como você deve ter notado, o algoritmo precisa sempre gerar as jogadas candidatas a partir de um estado inicial. Sendo assim, esse é um bom ponto de partida para a nossa implementação. Abaixo segue a implementação de uma função para gerar esses candidatos.
from copy import deepcopy
# ...
# FUNÇÔES ANTERIORES FICAM AQUI
# ...
def candidates(board, player):
candidate_moves = []
for i in range(len(board)):
for j in range(len(board)):
if board[i][j] != ' ':
continue
candidate = deepcopy(board)
candidate[i][j] = player
candidate_moves.append(candidate)
return candidate_moves
O que fazemos é, para cada posição livre no tabuleiro, criamos uma cópia desse tabuleiro e ocupamos a próxima posição possível. Com isso criamos uma lista de possíveis movimentos a partir de um estado inicial que foi passado para a função.
Em seguida precisamos de uma função para avaliar os nosso estados finais, ou seja, os estados onde o jogo acabou, seja por vitória, derrota ou empate.
def evaluate(board):
if is_win(board, CPU_PLAYER):
return 1
if is_win(board, HUMAN_PLAYER):
return -1
return 0
Estamos considerando o CPU_PLAYER como o MAX já que precisamos da melhor jogada para ele.
Com essa duas funções definidas já podemos começar a pensar na implementação do nosso Minimax. Como ele é recursivo, quem está familiarizado sabe, que a primeira coisa a ser definida é a condição de parada. No nosso caso verificamos se é um estado final e retornamos a avaliação.
def minimax(board):
if is_terminal(board):
return evaluate(board)
Para os estados intermediários precisamos saber se está na vez do MIN ou na vez do MAX, para tal, podemos passar um parâmetro chamado maximizing, assim saberemos se estamos maximizando ou minimizando. Colocaremos ele como False por padrão, apenas por fins de praticidade.
def minimax(board, maximizing=False):
if is_terminal(board):
return evaluate(board)
Agora precisamos definir o que o algoritmo vai fazer em cada turno. No caso do MAX temos que analisar as possibilidades e pegar a maior pontuação. A recursividade atrapalha um pouco esse processo já que não temos acesso a pontuação dos outros estados. Uma forma simples de fazer isso seria atribuir o menor valor possível para uma variável e sempre que uma pontuação for maior que ela nós atualizamos esse valor. Dessa forma vamos garantir que no retorno vamos manter sempre a maior prontuação. Essa implementação está ilustrado abaixo.
def minimax(board, maximizing=False):
if is_terminal(board):
return evaluate(board)
if maximizing:
value = float('-inf')
for child in candidates(board, CPU_PLAYER):
value = max(value, minimax(board, False))
return value
Note que quando o valor do maximizing for True precisamos passar para a próxima chamada o False para garantir que todos os turnos serão avaliados corretamente.
Para finalizar só precisamos fazer o mesmo para o MIN, só que com a lógica contrária, dessa vez vamos iniciar o valor com o número mais alto possível e pegar o mínimo entre as pontuações.
def minimax(board, maximizing=False):
if is_terminal(board):
return evaluate(board)
if maximizing:
value = float('-inf')
for child in candidates(board, CPU_PLAYER):
value = max(value, minimax(child, False))
else:
value = float('+inf')
for child in candidates(board, HUMAN_PLAYER):
value = min(value, minimax(child, True))
return value
Agora que já temos o nosso Minimax implementado e pronto para uso, só precisamos editar a nossa lógica de jogo. Para fazer isso é só substituir essa parte do código:
i, j = randint(0, 2), randint(0, 2)
while board[i][j] != ' ':
i, j = randint(0, 2), randint(0, 2)
board[i][j] = CPU_PLAYER
por esta outra parte:
candidate_moves = candidates(board, CPU_PLAYER)
board = max(candidate_moves, key=minimax)
O que estamos fazendo é gerar os candidatos para a próxima jogada do computador. Essas jogadas vão passar pela função max, que é nativa do Python. Com o parâmetro key ela vai calcular a pontuação de cada um dos candidatos e retornar o candidato com a maior pontuação. Dessa forma, nós vamos conseguir deixar o computador mais inteligente.
Você pode encontrar o código completo aqui. Esse arquivo já possui tanto o jogo da velha quanto o Minimax.
Otimizando com a poda Alfa-Beta
Você, possivelmente, está se perguntando porque chamamos a implementação anterior de ingênua. Se você executou o código da seção anterior deve ter notado uma demora para o computador executar a primeira jogada, principalmente se ele começar o jogo. Isso acontence por causa da quantidade de chamadas que ele faz para avaliar a árvore inteira. No jogo da velha para a primeira jogada, são mais de 500 mil chamadas executadas à função minimax. Acredito que você tenha percebido o problema nessa abordagem. No caso do Xadrez que para apenas 10 lances tem quase 70 trilhões de jogos possíveis, torna-se inviável de explorar toda a árvore de decisão.
Existem algumas formas de atenuar esse problema. Uma delas seria, sempre que detectarmos uma jogada que não vai acrescentar em nada a nossa solução, não precisamos expandir a partir dela, eliminando assim algum trabalho desnecessário. Mas como podemos detectar esse tipo de jogada? Nesse ponto entra a poda Alfa-Beta.
A poda Alfa-Beta é uma variação do algoritmo Minimax que visa reduzir a quantidade de estados que serão avaliados na árvore de busca.
A linha de pensamento é simples, Introduzimos duas novas variáveis alfa e beta, onde alfa é a melhor pontuação que já foi garantida para o MAX ao longo do caminho até o estado raiz, e beta é a melhor pontuação que já foi garantida para o MIN. Se estamos em um nível de MAX e ao longo de um caminho eu vejo que a pontuação gerada ao finalizar as verificações será menor que a garantida para o MAX, não faz sentido continuar expandindo dado que nunca vamos utilizá-la.
Achou difícil entender? Eu também! Talvez a implementação ajude você.
def minimax_alpha_beta(board, alpha=float('-inf'), beta=float('+inf'), maximizing=False):
if is_terminal(board):
return evaluate(board)
if maximizing:
value = float('-inf')
for child in candidates(board, CPU_PLAYER):
value = max(value, minimax_alpha_beta(child, alpha, beta, False))
if value >= beta:
break
alpha = max(alpha, value)
else:
value = float('+inf')
for child in candidates(board, HUMAN_PLAYER):
value = min(value, minimax_alpha_beta(child, alpha, beta, True))
if value <= alpha:
break
beta = min(beta, value)
return value
Não mudamos muito em relação ao código da seção anterior. A variáveis alfa e beta iniciam sempre com as piores pontuações possíveis para cada jogador, Infinito negativo e Infinito positivo respectivamente. Além disso inserimos novas verificações utilizando alfa e beta para quebar a cadeia recursiva quando não for vantajoso continuar expandido a partir dali.
Apenas com essas mudanças simples, conseguiremos reduzir a quantidade de chamadas recursivas de mais de 500 mil para pouco mais de 30 mil. Essa mudança reduziu em 94% o valor original.
Você pode encontrar o código completo aqui.
Aprimorando ainda mais com heurísticas
Mesmo conseguindo reduzir drasticamente a quantidade de nós expandidos, podemos tentar minimizar ainda mais o trabalho que o nosso algoritmo terá. Uma das formas mais simples de fazer isso seria utilizando uma limitação de profundidade. Essa limitação seria algo como uma fronteira, onde o nosso algoritmo só conseguiria olhar algumas jogadas a frente.
Essa solução é simples, mas nos trás um problema que não tinhamos antes. Como avaliar estados que ainda não finalizaram?
Essa pergunta é bem plausível, dado que se limitarmos a nossa visão, podemos não chegar até uma vitória, derrota ou empate. Que bom que temos uma solução para esse problema. Vamos utilizar uma heurística.
Uma heurística é qualquer abordagem ou método que não é garantidamente ótimo, perfeito ou racional, mas geralmente é o suficiente para atingir uma apoximação imediata de curto prazo. Quando uma solução perfeita é impossível ou impaticável, ela pode ser utilizada para otimizar o processo de encontrar uma solução satisfatória. A heurística pode ser um atalho mental que ajude na tomada de decisão.
Para o jogo da velha podemos elaborar uma heurística simples que vai nos dar uma pontuação para estados intermediários. Seria ela:
- Se o computador venceu, retorne Infinito positivo.
- Se o computador perdeu, retorne Infinito negativo.
- Para cada 2 símbolos na linha, coluna ou diagonal em favor do computador (uma posição vazia) soma +10
- Para 1 símbolo na linha, coluna ou diagonal em favor do computador (duas posições vazia) soma +1
- Pontuações negativas, -10 e -1 considerando as mesmas situações, só que a favor do oponente
- Caso contrário soma 0 (sequências vazias ou com simbolos do computador e do oponente ao mesmo tempo)
Com essa heurística podemos saber que, se a pontuação for positiva, quer dizer que o computador está em vantagem, se for negativa, o oponente está em vantagem, e no caso de ser 0 o jogo está empatado.
Segue a implementação para a nossa função heurística:
def evaluate_heuristic_sequence(sequence):
number_of_blank = sequence.count(' ')
has_two_simbols = (CPU_PLAYER in sequence and HUMAN_PLAYER in sequence)
if number_of_blank == 3 or has_two_simbols:
return 0
if number_of_blank == 2:
return 1 if CPU_PLAYER in sequence else -1
return 10 if CPU_PLAYER in sequence else -10
def heuristic(board):
if is_win(board, CPU_PLAYER):
return float('+inf')
if is_win(board, HUMAN_PLAYER):
return float('-inf')
score = 0
# Avaliando as linhas do tabuleiro
for line in board:
score += evaluate_heuristic_sequence(line)
# Avaliando as colunas do tabuleiro
for j in range(len(board)):
column = [board[i][j] for i in range(len(board))]
score += evaluate_heuristic_sequence(column)
# Avaliando as diagonais do tabuleiro
main_diag = [board[i][i] for i in range(len(board))]
secondary_diag = [board[i][j] for i, j in zip(range(3), range(2, -1, -1))]
score += evaluate_heuristic_sequence(main_diag)
score += evaluate_heuristic_sequence(secondary_diag)
return score
Dividimos a nossa implementação em duas funções apenas para fins de praticidade. A ideia é que a função evaluate_heuristic_sequence vai definir as regras da nossa heurística e a função heuristic vai verificar linhas colunas e diagonais para retornar a pontuação do estado que foi passado.
As mudanças dessa versão em relação a da seção Alfa-Beta são bem simples. Vamos adicionar uma variável para controlar a profundidade de expansão da árvore e trocar a função evaluate pela função heuristic.
def minimax_heuristic(board, depth=2, alpha=float('-inf'),
beta=float('+inf'), maximizing=False):
if depth==0 or is_terminal(board):
return heuristic(board)
if maximizing:
value = float('-inf')
for child in candidates(board, CPU_PLAYER):
value = max(
value,
minimax_heuristic(child, depth - 1, alpha, beta, False)
)
if value >= beta:
break
alpha = max(alpha, value)
else:
value = float('+inf')
for child in candidates(board, HUMAN_PLAYER):
value = min(
value,
minimax_heuristic(child, depth - 1, alpha, beta, True)
)
if value <= alpha:
break
beta = min(beta, value)
return value
Nesse trecho de código você vai notar que colocamos a verificação depth==0 para finalizar a execução quando atingirmos a profundidade máxima. Para garantir essa finalização precisamos decrementar essa variável nas próximas chamadas da função minimax_heuristic. Com essas mudanças vamos conseguir reduzir as chamadas recursivas ainda mais. Das 30 mil da seção anterior, passamos para pouco mais de 300 chamadas.
Uma coisa interessante de apontar é que, se você é um jogador entusiasta de jogo da velha, saberá que um jogador ótimo sempre começará o jogo nos cantos. No Minimax ingênuo e na abordagem com Alfa-Beta percebemos que isso fica bem visível quando deixamos o computador começar. Já nessa abordagem utilizando heurística e considerando a profundidade igual a 2, vemos que isso não acontece, porém o computador ainda é invencível. Essa é uma característica intrigante da utilização de heurísticas, nem sempre é garantido que vamos encontrar a solução ótima, dado que estamos flexibilizando o problema para poder resolvê-lo.
Você pode encontrar o código completo aqui.
Recapitulando...
O que fizemos hoje:
- Constuímos o nosso jogo da velha
- Entendemos o que é o Minimax e como ele pode ser utilizado
- Implementamos o Minimax padrão para o jogo
- Vimos que a implementação ingênua do Minimax tem certos problemas
- Implementamos otimizações
Conseguimos fazer o nosso algoritmo super inteligente para jogar o jogo da velha. Vimos que ele tem alguns problemas, mas com a técnica correta eles podem ser contornados. Sinta-se a vontade para procurar outras otimizações e quem sabe aplicar até em outros jogos. Um exercício interessante é pensar quais são os jogos em que ele pode ser aplicado.
Para você que acompanhou esse artigo até o final, muito obrigado pela sua atenção e até o próximo... bye bye